小４算数　授業報告　11月9日

小４算数　授業報告　11月9日

授業の前半の時間には、「小数の足し算と掛け算」と「3桁の整数を２桁の整数で割る割り算」を計算の課題として扱っています。どちらも、繰り返し練習して慣れる必要がありますので、継続して練習を行なってまいります。

後半では、前回（前回の授業のブログはこちら）に引き続き、ものの個数の数え方を題材に授業を行いました。前回の授業では、「問題文を読んで直感的に思ったことが、必ずしも正しいとは限らない」ということを体験してもらい、その上で「考えたことが正しいかどうかを確認する必要がある」ということを感じてもらいました。確認の際には、図を書いた上で、その図をよく観察して考えるように指示をしました。今回の授業でも、図を書いて観察するという行動を身につけるための練習を行いました。

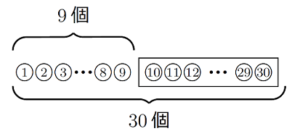
この問題では⑩が１個目、⑪が２個目と、ボールに書かれている番号とそのボールが「左から何個目であるか」の間にずれがあります。もし、ボールに書かれている番号が①から始まっていれば、①が１個目、②が２個目とボールに書かれている番号と「ボールが左から何個目であるか」が一致するため、非常に見通しが良くなります。ここまでは、番号のついたものの個数を数えるときに知っておくべきことです。ここから先については自分で考えることが必要です。

問題を解くときに、自分が読んだことを確認し、考える手がかりにするために、問題文から読み取ったことを図や表にして表現することは有効です。問題文に書かれていることを図に書いて整理する段階で、見通しをよくするために、番号が①から始まるようにボールを書き足すことができれば(下図参照）、後は図を観察して考えることで何をすべきかがわかるようになります。

ただ「①から始まるようにボールを書き足す」ということに自分ひとりで気付くことは現時点では難しいので、自力でたどり着けなかった場合には、解決のためのヒントを出して考えてもらいました。

（例題１）ができるようになったお子様には、

同じテーマについて、逆方向からアプローチした問題に挑戦してもらいました。
逆方向から同じテーマを扱うときは、逆方向からの問題を直接説明することはしません。これをしてしまうと、逆方向の問題を前に取り扱った問題とはまったく「別のもの」と認識してしまい、それぞれの問題の解き方を覚える方向に意識が向いてしまうからです。

この問題を、初めて見る問題と感じて、どうしていいのかわからないと思って手が止まってしまうこともあるかもしれません。しかし、番号のついたボールについて、番号と個数の関係が問われていることは分かれば、（例題１）と同様、図を書いて整理することによって、何をすべきかがわかるようになります。

何人かのお子様は（例題２）についても、①から数えられるように書き足して考えることで、正解にたどり着いていました。良い経験をしてくれたと思います。

問題文から読み取ったことを図に書き表し、その図をよく観察するという行動をとれることはとても大切です。見たことがないような問題でも考えられるようになるために、今後の授業においても上記の行動の重要性を繰り返し経験してもらいます。